Orthographic Projections, Continued
Circles, arcs,
and ellipses
(Continued)
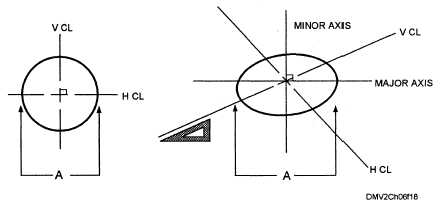
Ellipses have two axes, a major axis (long) and a minor axis (short). When
the horizontal and vertical centerlines of a circle drawn parallel to the plane
of projection is drawn in isometric and each has parallel tangents, they
become conjugate diameters representing the major and minor axes,
respectively. The two diameters of an ellipse are conjugate when each is
parallel to the tangents at the ends of the other. One of a given pair of given
conjugate diameters is, as a rule, not perpendicular to the other. In general,
here are three rules to remember when drawing ellipses in isometric, (1) the
major axis of an ellipse is equal to the diameter of the circle, (2) the major
axis of the ellipse is always at right angles to the centerline of the circle, and
(3) the minor axis is at right angles to the major axis, which coincides with
the centerline of the circle. ‘Another way of drawing ellipses in isometric is
to use an ellipse template. Ellipse templates are available in many different
degrees with the major and minor axes marked on the template. Base your
selection of the appropriate ellipse on the location and degree of the axes.
Figure 6-18 shows the relationship of the conjugate diameters of a circle to
the major and minor axes of an ellipse.
Figure 6-18.—Major and minor axes.
Offset
Offset measurements are measurements used to locate features or edges with
measurements
respect to the features and edges on the main surface of the object. Feature
and edges parallel to edges of the main surface remain parallel in isometric
drawings.
Continued on next page
6-23